Juegos de geometría

JUEGOS

FORMANDO TRIÁNGULOS

Juego	Formando triángulos
Material	Lápiz, hoja y regla
Nº de jugadores	individual

 • Reglas del juego: Si tienes una hoja de papel en blanco y dibujas una recta no se forma ningún triángulo. Si dibujas dos sigue sin haberlos. Con tres rectas ya se puede formar un triángulo, aunque según como estén situadas las rectas no formen ninguno (por ejemplo cuando dos son paralelas). Es decir, que tres rectas forman como máximo un triángulo. Con cuatro rectas ya se pueden formar muchos triángulos. Se trata, en primer lugar, que busques el número máximo de triángulos que se pueden formar con cuatro rectas. Una vez que lo tengas, tienes que hacer lo mismo con cinco rectas. Después con seis. Y así seguir mientras lo consideres necesario, hasta llegar al caso general: obtener el número máximo de triángulos que se pueden formar con un número cualquiera n de rectas.

 • Posibles variantes: En las primeras aproximaciones al juego se puede limitar el número de rectas hasta el número que se considere oportuno (6 u 8, por ejemplo). Y dibujar además, no solo la configuración que permite obtener el mayor número de triángulos, sino también otras que forman menos triángulos, e investigar las posibilidades que existan.

PUZLE: CUADRADO DE LAS SIETE PIEZAS

Aquí tienes en una cuadrícula unidad, las siete piezas de un puzle tipo tangram. Con todas ellas se puede formar un gran cuadrado.

Puedes asignarle la medida que quieras a las líneas discontinuas, todas son iguales.

 

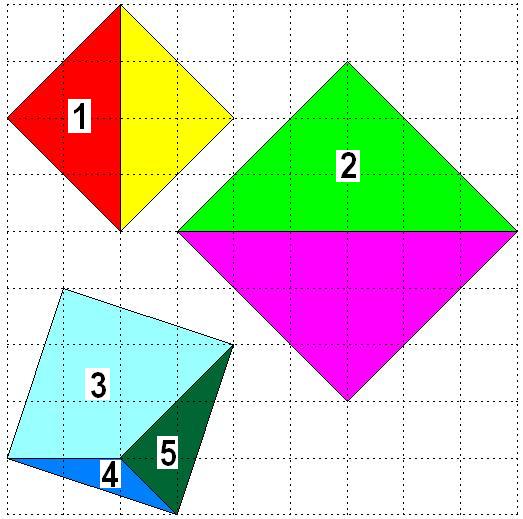
1. Calcula las áreas de los tres cuadrados.

 2. Calcula el área del cuadrado grande que se puede obtener juntando las siete piezas. ¿Cuál será su lado? 

3. ¿Alguna de las 7 piezas tiene un lado igual? Recorta tus piezas y construye el cuadrado grande.

El EXTRATERRESTRE DE PITÁGORAS

Este extraño animal tiene la propiedad que su pie cuadrado rojo tiene la misma superficie que todas sus otras partes rojas.

. ¿Sabrías explicar por qué?

PUZLE HEXAGONAL DE CÁLCULO DE VOLÚMENES

Presentamos aquí 24 fichas triangulares. Cada triángulo lleva sobre uno, dos o tres de sus lados una pregunta y en otros el resultado del cálculo asociado a la pregunta.

Estos son las preguntas utilizadas:

Material necesario:

– 24 fichas triangulares por alumno o por pareja de alumnos.

Reglas del juego: Se trata de un juego para parejas cooperativas.

– Cada pareja debe intentar unir los lados de los triángulos juntando cada pregunta con el resultado correspondiente. De esta forma se puede formar un gran hexágono.

Metodología:

 Por parejas, se resolverán las preguntas propuestas y se anotará el resultado en una tabla parecida a la de arriba.

1. Una vez resueltas las preguntas, comprobarán sus resultados con los de otra pareja para asegurar que las operaciones se han resuelto correctamente.
2. Una vez comprobados los resultados, escribirán en las piezas del puzle los resultados y recortarán las piezas

Banderas Algebraicas

Observaciones: Observando unas banderas, se presentan tres problemas algebraicos muy sencillos.

Ejercicio 1:

Con estos cuatro rectángulos idénticos de perímetro 112 cm, se obtiene esta curiosa bandera rectangular.

¿Cuánto ocupa la bandera desplegada?

Ejercicio 2:

Con estos seis rectángulos idénticos se ha formado ahora esta gran bandera:

¿Si la altura de la bandera es de 21 cm, cuánto ocupa la bandera desplegada?

Ejercicio 3.

Con cuatro cuadrados, dos de ellos iguales se ha formado esta nueva bandera que tiene de base 2m (200 cm):

¿Cuánto ocupa la bandera desplegada?